PROYECCIONES

PROYECCIÓN DIÉDRICA DE PUNTOS

Proyección Diédrica de un Punto

Se denomina así a la representación de las proyecciones ortogonales de un punto, sobre los planos vertical y horizontal de proyección en forma simultanea.

los puntos se denominan con letras mayúsculas (A,B,C,...Z) o con números (1,2,3...).

PROYECCIÓN DIÉDRICA DE RECTAS

Proyección Diédrica de una Recta

Las rectas se designan con letras minúsculas (a; b; c;...).
Una recta (r) puede ser definida por medio de dos puntos (A y B)

Proyección diédrica de una recta

Punto Contenido en una Recta

Si un punto (P) esta contenido en una recta (r), entonces las proyecciones vertical (P^v) y horizontal (P^h) del punto están contenidas en las proyecciones vertical (r^v) y horizontal (r^h) de la recta, respectivamente.

Trazas de una Recta

Son los puntos donde la recta se intercepta con los planos principales de proyección; se denominan:

• traza vertical: punto donde la recta se intercepta con el plano vertical de proyección. Generalmente se designa con la letra (V).
• traza horizontal: punto donde la recta se intercepta con el plano horizontal de proyección. Generalmente se designa con la letra (H).

trazas de una recta

Recta Horizontal

Es una recta paralela al plano horizontal de proyección; por lo tanto, se proyecta sobre este plano en verdadero tamaño; su proyección vertical es paralela a la línea de tierra, por que todos sus puntos tienen igual cota (Z=cte.), y por lo tanto forma un ángulo de cero grados con el plano horizontal de proyección (a^o=0⁰).

Recta Frontal

Es una recta paralela al plano vertical de proyección; por lo tanto, se proyecta sobre este plano en verdadero tamaño; su proyección horizontal es paralela a la línea de tierra, por que todos sus puntos tienen igual vuelo (Y=cte.), y por lo tanto forma un ángulo de cero grados con el plano vertical de proyección (b^o=0⁰).

Recta Paralela a la Línea de Tierra

Es una recta paralela simultáneamente a los planos vertical y horizontal de proyección; por lo tanto, es una recta horizontal y frontal, y en consecuencia tiene las propiedades de ambas; es decir, su cota es constante (Z=cte) y su vuelo también (Y=cte). Sus proyecciones horizontal y vertical son paralelas a línea de tierra; están en verdadero tamaño; y forman ángulos de cero grados con los planos vertical y horizontal de proyección (a^o=b^o=0⁰).

Recta Vertical

Es una recta perpendicular al plano horizontal de proyección; por lo tanto, su proyección horizontal es un punto, y su proyección vertical se observa en verdadero tamaño y perpendicular a línea de tierra; forma ángulos de noventa grados con el plano horizontal de proyección (a^o=90⁰) y cero grados con el plano vertical de proyección (b^o=0⁰).

Recta de Punta

Es una recta perpendicular al plano vertical de proyección; por lo tanto, su proyección vertical es un punto, y su proyección horizontal se observa en verdadero tamaño y perpendicular a línea de tierra; forma ángulos de cero grados con el plano horizontal de proyección (a^o=0⁰) y noventa grados con el plano vertical de proyección (b^o=90⁰).

Recta de Perfil

Es una recta perpendicular a la línea de tierra (paralela al plano lateral); sus proyecciones son perpendiculares a línea de tierra. Su verdadero tamaño, así como los ángulos que forma con los planos principales de proyección, pueden determinarse en una proyección lateral de la misma.

Formas de definir un plano

Un plano (a) puede definirse por medio de:

 a)     Tres puntos (A; B; y C)\ Fig.2.

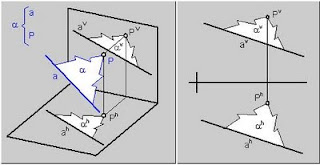
b)    Una recta (a) y un punto (P)\ Fig.3.

Fig.3.\ Plano (a) definido por una recta (a) y un punto (P)

c)     Dos rectas (a y b) que se cortan\ Fig.4.

Fig.4.\ Plano (a) definido por dos rectas (a y b) que se cortan

d)    Dos rectas (a y b) paralelas\ Fig.5.

Fig.5.\ Plano (a) definido por dos rectas (a y b) paralelas

Dos rectas que se cruzan no definen un plano\ Fig.6.

Fig.6.\ Dos rectas (a y b) que se cruzan no definen un plano

Un plano, inicialmente definido por tres puntos (Fig.7a), puede posteriormente ser definido por: una recta (a) y un punto (A) (Fig.7b1); dos rectas (a y b) que se cortan (Fig.7b2); o dos rectas (a y b) paralelas (Fig.7b3).

Trazas de un Plano

Son las rectas donde el plano se intercepta con los planos principales de proyección. Se denominan\ Fig.11:

a)     Traza vertical de un plano. Es la intersección (f) del plano (a) con el plano vertical de proyección\Fig.11a.

b)    Traza horizontal de un plano. Es la intersección (h) del plano (a) con el plano horizontal de proyección\ Fig.11b.

Las trazas (f y h) de un plano (a) se cortan en la línea de tierra (excepto si el plano (a) es paralelo a ella).

DETERMINACIÓN DE LAS TRAZAS DE UN PLANO

Si una recta (r) está contenida en un plano (a); las trazas vertical (V) y horizontal (H) de la recta (r), están contenidas en las trazas vertical (f) y horizontal (h) del plano (a), respectivamente (fig.12). Además, como ya se mencionó, las trazas de un plano se cortan en la línea de tierra (Excepto si el plano es paralelo a ella).

fig.12.\ Trazas de una recta (r) contenida en un plano (a)

Por lo tanto, pueden definirse las trazas de un plano (a), definiendo previamente las trazas de dos rectas (a y b) contenidas en el, como se muestra en los ejemplos (a) y (b) de la fig.13.

fig.13.\ Determinación de las trazas de un plano\ ejemplos

PUNTO QUE PERTENECE A UN PLANO DEFINIDO POR TRAZAS

En la figura siguiente, se ilustra como hacer pertenecer un punto (P) a un plano (a) definido por trazas (f y h)\ (fig.a), utilizando para ello:

• una recta: (r) cualquiera (fig.b1);
• una recta (f¹) frontal (fig.b2);
• una recta (h¹) horizontal (fig.b3).

Punto contenido en un plano definido por trazas

Rectas Características de un Plano

Se llaman rectas características de un plano (a) a  las rectas del plano que son paralelas a uno de los planos principales de proyección. Se denominan\ fig.14:

a)     Rectas características frontales de un plano. Son las rectas (f¹) del plano (a) paralelas al plano vertical de proyección; en consecuencia son paralelas a la traza vertical (f) del plano a\ fig.14a.

fig.14.\ Rectas características de un plano

Todas las rectas frontales (f; f¹; f²; ...) de un plano (a) son paralelas entre sí\ fig.15.

fig.15.\ Paralelismo entre rectas características frontales

b)    Rectas características horizontales de un plano. Son las rectas (h¹) del plano (a) paralelas al plano horizontal de proyección; en consecuencia son paralelas a la traza horizontal (h) del plano (a)\ fig.14b.

Todas las rectas horizontales (h; h¹; h²; ...) de un plano (a) son paralelas entre sí\ fig.16.

fig.16.\ Paralelismo entre rectas características horizontales

Un plano (a) puede ser definido por dos rectas características (f¹ y h¹), como se muestra en la fig.17a. Y las trazas (f y h) de este plano (a), pueden determinarse a partir de sus rectas características (f¹ y h¹), como se muestra en la fig.17b.

PUNTO QUE PERTENECE A UN PLANO DEFINIDO POR RECTAS CARACTERÍSTICAS

En la fig.18, se ilustra como hacer pertenecer un punto (P) a un plano (a) definido por rectas características (f y h) (fig.18a); utilizando para ello:

• una recta: (r) cualquiera (fig.18b1);
• una recta (f¹) frontal (fig.18b2);
• una recta (h¹) horizontal (fig.18b3).

fig.18.\ Punto que pertenece a un plano definido por rectas características

Planos en Posiciones Particulares

Los planos, al igual que las rectas, pueden ocupar ciertas posiciones particulares con respecto a los planos principales de proyección. El estudio de estas posiciones es muy importante; ya que poseen propiedades proyectivas propias que permiten simplificar la resolución de problemas relacionados con este tipo de planos.

En las fig.22 a fig.24, se muestran estas posiciones particulares. Los puntos (A; B; y C) representados en cada caso están contenidos en el plano (a) mostrado, y se indican además los ángulos (a⁰ y b⁰) que el plano (a) forma en cada caso con los planos horizontal  y vertical de proyección respectivamente. A continuación, se hace una breve descripción de estas posiciones particulares:

a)     Plano frontal. Es un plano paralelo al plano vertical de proyección; por lo tanto todos sus puntos tienen el mismo vuelo. Su traza horizontal, sobre la cual se proyecta horizontalmente todo el plano, es paralela a la línea de tierra. El plano se proyecta verticalmente en verdadero tamaño\ fig.22a.

b)    Plano horizontal. Es un plano paralelo al plano horizontal de proyección; por lo tanto todos sus puntos tienen la misma cota. Su traza vertical, sobre la cual se proyecta verticalmente todo el plano es paralela a la línea de tierra. El plano se proyecta horizontalmente en verdadero tamaño\ fig.22b.

c)     Plano vertical. Es un plano perpendicular al plano horizontal de proyección; por lo tanto su traza vertical es perpendicular a la línea de tierra, todo el plano se proyecta horizontalmente sobre su traza horizontal\ fig.22c.

fig.22.\ Planos en posiciones particulares

d)    Plano de punta. Es un plano perpendicular al plano vertical de proyección; por lo tanto su traza horizontal es perpendicular a la línea de tierra, todo el plano se proyecta verticalmente sobre su traza vertical\ fig.22d.

e)    Plano de perfil. Es un plano perpendicular a la línea de tierra; por lo tanto es paralelo al plano lateral y en consecuencia todos sus puntos tienen igual distancia a este plano. Sus trazas horizontal y vertical son perpendiculares a la línea de tierra, y todo el plano se proyecta horizontal y verticalmente sobre ellas. El plano se proyecta lateralmente en verdadero tamaño, por eso es frecuente en estos planos determinar su proyección lateral\ fig.22e.

f)      Plano paralelo a la línea de tierra. Sus trazas son paralelas a la línea de tierra\ fig.22f.

g)  Plano que pasa por la línea de tierra. Sus trazas se encuentran en la línea de tierra, la cual es una recta del plano\ fig.23. Todas las rectas contenidas en estos planos se cortan con la línea de tierra (excepto si son paralelas a ella). Existen además dos planos muy particulares de este tipo denominados:

fig.23.\ Plano que pasa por la la línea de tierra

1)    Primer bisector. Es un plano que pasa por la línea de tierra y forma 45⁰ con el plano horizontal de proyección, dividiendo en partes iguales a los cuadrantes uno (I C) y tres (III C). Las proyecciones de cualquier figura geométrica contenida en el primer bisector son simétricas; debido a que para todos sus puntos: la cota, es igual al vuelo\ fig.24a.

fig.24.\ Planos bisectores

 

2)    Segundo bisector. Es un plano que pasa por la línea de tierra y forma 45⁰ con el plano horizontal de proyección. dividiendo en partes iguales a los cuadrantes dos (II C) y cuatro (IV C). Las proyecciones de cualquier figura geométrica contenida en el segundo bisector son coincidentes; debido a que para todos sus puntos: la cota y el vuelo son iguales en magnitud pero diferentes en signo\ fig.24b.

INTERSECCIÓN

Intersección entre una Recta y un Plano

La intersección entre una recta (r) y un plano (a) es un punto (I)\ fig.1.

fig.1.\ Intersección (I) entre una recta (r) y un plano (a)

DETERMINACIÓN DE LA INTERSECCIÓN ENTRE UNA RECTA Y UN PLANO (recta tapada)

Para definir el punto de intersección (I) entre una recta (r) y un plano (a), se aplica un procedimiento denominado recta tapada, el cual consiste en:\ fig.2:

a)     Definir en el plano (a) una recta (t), cuya proyección horizontal (t^h) coincide (se tapa) con la proyección horizontal (r^h) de la recta (r); por esta razón la recta (t) se denomina recta tapada. Las rectas (r y t) se cortan en el punto de intersección (I) buscado.

fig.2.\ Determinación de la intersección (I), entre recta (r)  y plano (a), tapando las proyecciones horizontales (r^h y t^h) de las rectas (r y t)

b)    La proyección vertical (I^v) del punto (I) queda definida por el corte de las proyecciones verticales (r^v y t^v) de las rectas (r y t).

c)     La proyección horizontal (I^h) del punto (I), se obtiene proyectivamente, sobre la proyección horizontal (r^h=t^h) de las rectas (r y t).

También es posible definir la intersección (I) entre una recta (r) y un plano (a) tapando las proyecciones verticales (r^v y t^v) de las rectas (r y t) y siguiendo un procedimiento análogo al anterior\ fig.3.

fig.3.\ Determinación de la intersección (I) entre una recta (r)

 y un plano (a), tapando las proyecciones

 verticales (r^v y t^v) de las rectas (r y t)

Ejemplo 1: Definir la intersección (I), de la recta (r), con el plano (a), definido por sus trazas\ fig.4a.

Solución: En la fig.4b, se muestra la solución tapando las proyecciones horizontales (r^h=t^h) de las rectas (r y t) y en la fig.4c, tapando sus proyecciones verticales (r^v=t^v).

fig.4.\ Intersección (I) de la recta (r) con el plano (a) definido por trazas

Ejemplo 2: Definir la intersección (I), de la recta (r), con el plano (a), definido por sus rectas  (f y h) características\ fig.5a.

Solución: En la fig.5b, se muestra la solución tapando las proyecciones horizontales (r^h=t^h) de las rectas (r y t) y en la fig.5c, tapando sus proyecciones verticales (r^v=t^v).

fig.5.\ Intersección (I) de la recta (r) con el plano (a) definido por rectas características (f y h)

Ejemplo 3: Definir la intersección (I), de la recta (r), de perfil, con el plano (a), definido por sus sus trazas\ fig.6a.

Solución: El punto de intersección (I), puede definirse en una proyección lateral del sistema\ fig.6b.

fig.6.\ Intersección (I) de un plano (a) definido por trazas, con una recta (r) de perfil

Ejemplo 4: Definir la intersección (I), de la recta (r), con los planos bisectores\ fig.7a.

Solución:

intersección de la recta con el primer bisector: En la fig.7b, se muestra como definir la intersección (I) de la recta (r) con el primer bisector, en el cual las proyecciones de la recta (t) son simétricas.

intersección de la recta con el segundo bisector: En la fig.7c, se muestra como definir la intersección (I) de la recta (r) con el segundo bisector, en el cual las proyecciones de la recta (t) coinciden.

fig.7.\ Intersección (I) de una recta (r) con los planos bisectores

Análisis de la Visibilidad, en la Intersección de una Recta con un Plano

La representación de la intersección de una recta (r) con un plano (a), siempre presenta dos posibilidades de visibilidad, como se muestra en las fig.8a y fig.8b, en las cuales puede observarse que un segmento de la recta (r), definido por el punto de intersección (I) y un punto del contorno del plano (a), permanece invisible al observador, siendo tapado por el plano.

En Doble Proyección Ortogonal, debe analizarse la visibilidad en las proyecciones horizontal y vertical en forma independiente, debido a que los segmentos visibles en una de las proyecciones no son necesariamente visibles en la otra proyección.

Por medio del siguiente ejemplo se describe la forma de analizar la visibilidad en la intersección de una recta (r) con un plano (a).

Ejemplo: Definir la intersección (I) y visibilidad entre la recta (r) y el triángulo de vértices (A;B; y C)\ fig.9a.

Solución:

a)  Se determina el punto de intersección (I) entre la recta (r) y el triángulo (A;B;C)\ fig.9b.

fig.9.\ Intersección entre recta y plano\ VISIBILIDAD

b) Para determinar la visibilidad en proyección vertical\ fig.9c:

1)  Se define el segmento de punta (1-2) cuya proyección vertical (1^v=2^v) es el punto de corte entre las proyecciones verticales de la recta (r) y del lado (A-B). Estando los puntos (1 y 2) contenidos en:

punto 1: En el lado (A-B).

punto 2: En la recta (r).

2)  De estos dos puntos, solo uno es visible en proyección vertical, y será aquel de los dos que posea mayor vuelo. Por lo tanto se define la proyección horizontal del segmento de punta (1-2), y se determina en ella cual de estos dos puntos tiene mayor vuelo; resultando ser el punto (2).

Se define entonces, que el segmento (2-I) de la recta (r) es visible en proyección vertical, porque el punto (2) que esta contenido en el es visible en esta proyección.

c)  Para determinar la visibilidad en proyección horizontal\ fig.9d:

1)  Se define el segmento vertical (3-4) cuya proyección horizontal (3^h=4^h) es el punto de corte entre las proyecciones horizontales de la recta (r) y del lado (B-C). Estando los puntos (3 y 4) contenidos en:

punto 3: En el lado (B-C).

punto 4: En la recta (r).

2)  De estos dos puntos, solo uno es visible en proyección horizontal, y será aquel de los dos que posea mayor cota. Por lo tanto se define la proyección vertical del segmento vertical (3-4), y se determina en ella cual de estos dos puntos tiene mayor cota; resultando ser el punto (4).

Se define entonces, que el segmento (4-I) de la recta (r) es visible en proyección horizontal, porque el punto (4) que esta contenido en el es visible en esta proyección.

Intersección entre dos Planos

La intersección entre dos planos (a y b) es una recta (i), para determinarla\ fig.10a:

a)     Se elige, cualquier recta (a) en el plano (a), y se determina su intersección (I) con el plano (b).

b)    Se repite el paso anterior eligiendo una segunda recta, (b) en el plano (a), y determinando su intersección (J) con el plano (b).

fig.10.\ Intersección (i) entre dos planos (a y b)

c)     Los puntos de intersección (I y J) definen la recta de intersección (i) entre los planos (a y b).

Las rectas (a y b) también pueden ser elegidas en el plano (b) y ser interceptadas con el plano (a)\ fig.10b.

Ejemplo 1: Definir la intersección (i) entre los planos (a y b), definidos por sus trazas\ fig.11a.

Solución: Se definen dos rectas (a y b) frontales del plano (a), y se determinan sus intersecciones (I y J) con el plano (b). La recta de intersección (i) entre los planos (a y b) queda definida por los puntos (I y J)\ fig.11b.

fig.11.\ Intersección (i), entre dos planos (a y b) definidos por trazas

Ejemplo 2: Definir la intersección (i) entre el plano (a), definido por sus trazas y el plano (b), definido por las rectas (a y b) paralelas\ fig.12a.

Solución: La intersección (I) entre los planos (a y b), queda definida por los puntos de intersección (I y J) de las rectas (a y b) con el plano (a)\ fig.12b.

fig.12.\ Intersección (i), entre un plano (a) definido por trazas, y un plano (b) definido por rectas (a y b) paralelas

Ejemplo 3: Definir la intersección (i) entre el plano (a), definido por sus rectas (f y h), características y el plano (b), definido por las rectas (a y b), paralelas\ fig.13a.

Solución: La intersección (I) entre los planos (a y b), queda definida por los puntos de intersección (I y J) de las rectas (a y b) con el plano (a)\ fig.13b.

fig.13.\ Intersección (i), entre un plano (a) definido por rectas (f y h) características, y un plano (b) definido por rectas (a y b) paralelas

Ejemplo 4: Definir la intersección (i) entre el plano (a), definido por sus trazas y el plano (b), que pasa por la línea de tierra y contiene al punto (A)\ fig.14a.

Solución:

1)  Se traza, por el punto (A), una recta (r) cualquiera del plano (a); es decir, cualquier recta (r) que pase por el punto (A) y se corte con la línea de tierra\ fig.14b.

2)  Se define la intersección (I) de la recta (r) con el plano (a).

3)  Se define la intersección (J) del plano (a) con la línea de tierra.

4)  Los puntos (I y J) están contenidos simultáneamente en los planos (a y b), por lo tanto definen a la recta de intersección (I) entre ambos planos.

fig.14.\ Intersección (i) de un plano (a) definido por trazas, con un plano (b) que pasa por la línea de tierra y contiene a un punto (A)

Análisis de la Visibilidad en la Intersección de dos Planos

Ejemplo: Definir la intersección y visibilidad entre el triángulo (A;B;C) y el cuadrilátero (1;2;3;4) contenido en el plano (1;2;3)\ fig.15a.

Solución:

a)     Se define la proyección horizontal (1^h) del vértice (1), haciéndolo pertenecer al plano (1;2;3)\ fig.15b.

fig.15.\ Intersección y visibilidad de dos planos\ ejemplo

b)    Se definen las intersecciones: (I) de la recta (A-B) con el cuadrilátero (1;2;3;4); y (J) de la recta (2-3) con el triángulo (A;B;C). El segmento (I-J) pertenece a los dos planos, y si está contenido en el primer cuadrante siempre es visible en ambas proyecciones\ fig.15c.

c)     Se define la visibilidad de la intersección entre las dos figuras planas, por medio del análisis de visibilidad de la intersección de las rectas: (A-B) con el cuadrilátero (1;2;3;4); y (2-3) con el triángulo (A;B;C)\ fig.15d.

Intersección entre tres Planos

La intersección de tres planos (a; b; y g) es un punto (I). El cual se define interceptando, con el plano (g), la recta de intersección (i) entre los planos (a y b)\ fig.16.

fig.16.\ Intersección (I) entre tres planos (a, b y g)

Ejemplo: Definir la intersección (I) entre los planos (a; b; y g)\ fig.17a.

Solución:

a)     Se determina la intersección (i) entre los planos (a y b)\ fig.17b.

b)    Se determina la intersección (I) de la recta (i) con el plano (g)\ fig.17c.

  

fig.17.\ Intersección (I) de tres planos\ ejemplo



fig.8.\ Intersección entre una recta y un plano\ VISIBILIDAD

fig.17.\ Plano (a) definido por rectas (f¹ y h¹) características

Fig.11.\ Trazas de un plano

Fig.7.\ Cambio de la definición original de un plano

Fig.2.\ Plano (a) definido por tres puntos (A; B; y C)